La radice quadrata di 4 si ricava ottenendo quel numero che elevato al quadrato, quindi moltiplicato per sé stesso, dà come risultato 4. Il risultato semplicemente è 2 e vedremo anche come è facile da dimostrare e da risolvere. Dato che 2 è un numero intero, diciamo che 4 è un quadrato perfetto.
Un radicale è l’operazione matematica inversa della potenza. Consiste nel trovare, se esiste, quel numero che elevato all’indice scritto in alto a sinistra della radice darebbe il numero che c’è dentro la radice.
Per semplificare una radice è possibile scomporre il numero all’interno, chiamato radicando, in fattori primi ottenendo delle potenze i cui esponenti potrebbero semplificarsi con l’indice. Il primo passaggio da fare, quindi, è quello di scomporre il numero 4 e riscriverlo sotto forma di potenza all’interno della radice. A quel punto, sarà molto facile semplificare l’espressione dato che l’indice e l’esponente del radicando saranno uguali e si annulleranno a vicenda.
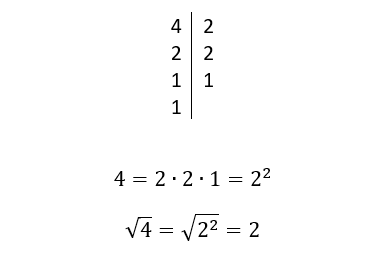
Dalla dimostrazione abbiamo visto che il numero 4 è scomponibile in 2 ∙ 2, cioè 22. Dato che adesso l’esponente del radicando è 2 e l’indice della radice è 2 e che la radice è l’inverso della potenza, questi si annulleranno a vicenda dandoci il risultato della radice quadrata di 4.



