L’errore relativo di una misurazione

L’errore relativo di una misurazione è il rapporto tra l’errore assoluto dovuto al limite dello strumento usato nelle misurazioni e il valore più preciso ottenuto con questo strumento.

Nella vita quotidiana, a scuola o al lavoro abbiamo sempre bisogno di misurare qualche grandezza. Può essere la massa di un ingrediente, la lunghezza dei lati di un poligono o quelli di una stanza. In tutti questi casi, comunque, non abbiamo bisogno di calcolare l’errore perché ci basta la misurazione fatta con lo strumento che abbiamo.

Comunque sia, è impossibile risalire alla misura vera, assoluta, di una qualsiasi grandezza. Ogni strumento di misurazione ha un limite minimo, chiamato sensibilità, e un limite massimo, chiamato portata, di misurazione.

Le bilance usate per gli alimenti possono avere come sensibilità una decina di grammi e come portata non più di qualche chilo mentre quella usata per pesare le persone ha un limite minimo di misurazione così alto che non percepirebbe la massa di un chilo di farina.

Come si calcola l’errore relativo

Per calcolare l’errore relativo e assoluto di una misurazione è necessario tenere conto della sensibilità dello strumento. Per comodità, vedremo come si fa su un rettangolo disegnato in un foglio a quadri, dove il lato di un singolo quadrato sarà la nostra unità di misura che chiameremo 1l.

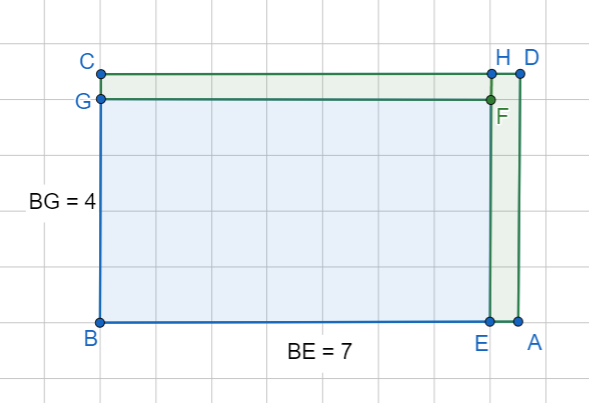
Non è possibile assegnare un valore assoluto ai due lati, perché entrambi finiscono all’interno di un quadrato. La base misura tra 7 l e 8 l mentre l’altezza equivale alla somma di 4 l e il suo errore assoluto. Dato che la sensibilità della nostra misurazione è 1 l considereremo come valore più attendibile la sua metà e diremo che:

• La base AB misura (7,5 ± 0,5) l; il lato ha una misura minima di 7 l e una massima di 8 l
• Il lato BC misura (4,5 ± 0,5) l; la sua misura ha un valore minimo di 4 l e uno massimo di 5 l

L’errore relativo è quindi il rapporto tra l’errore assoluto della misurazione e la misura più vicina a quella vera e la sua formula si può scrivere così: e_r = e_a/M.

Calcoliamo l’errore relativo dei lati del rettangolo e lo arrotondiamo a due cifre decimali:

• e_r1 = e_a1/M₁ = 0,5 l/7,5 l = 0,07
• e_r2 = e_a2/M₂ = 0,5 l/4,5 l = 0,11

Se vogliamo ricavare l’errore di misurazione dell’area del rettangolo dobbiamo sommare quelli relativi ai suoi lati e moltiplicarla per la superficie che è possibile misurare.

• e_r = e_r1 + e_r2 = 0,18
• A = (7,5 ∙ 4,5) l² = 33,75 l² = 34 l²
• e_r = e_a / A;
  • e_a = e_r ∙ A = 0,18 ∙ 34 l² = 6,12 l² = 6 l²

L’area del rettangolo ABCD è uguale a (34 ± 6) l² ed è compreso tra 28 l² e 40 l².

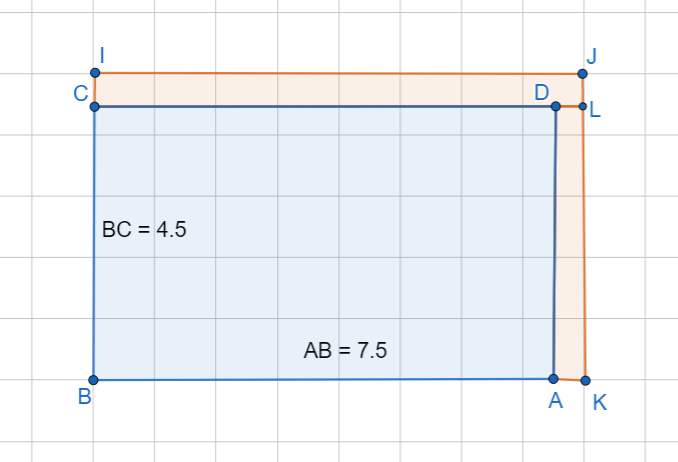
Questo è dimostrato anche facendo la somma delle aree dei due rettangoli che rappresentano gli errori assoluti:

• A_CIJL = 7,5 l ∙ 0,5 l = 4 l²;
• A_ADLK = 4,5 l ∙ 0,5 l = 2 l²;
• e_a = A_CIJL + A_ADLK = 6 l²;
  • e_r = e_a / A_ABCD = 6 l² / 34 l² = 0,18 ;

Se moltiplichiamo l’errore relativo per 100 otterremo l’errore percentuale. Così possiamo dire che l’errore di misurazione della base del rettangolo è del 7%, quello dell’altezza è dell’ 11% e quello dell’area è del 18%.

Questa grande differenza tra il valore minimo e quello massimo della superfice del rettangolo mostra quanto è importante avere a disposizione uno strumento di misurazione con il più basso livello di sensibilità e il più preciso possibile perché tutti i calcoli successivi avranno errori maggiori.