La somma il prodotto delle soluzioni di un’equazione ridotta in forma normale come ax2 + bx + c = 0 sono facilmente ricavabili anche senza conoscere il valore delle loro incognite.
Per ricavare la somma e il prodotto delle soluzioni, dobbiamo applicare la formula risolutiva. In questo caso ci basta riscrivere la formula per ogni incognita e fare le operazioni algebriche. Nel primo caso, sommiamo le due formule, nell’altro le moltiplichiamo.
Se abbiamo a che fare con equazioni letterali, ci basta ricordare che una terza soluzione è sempre uguale a 0, e succede se il parametro del termine di secondo grado è uguale a 0. Poi per ricavare le altre due soluzioni possiamo procedere normalmente.
Perciò, per ricavare la somma delle due soluzioni dobbiamo sommare le due formule risolutive.
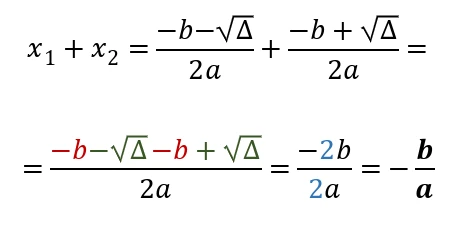
Per ricavare il prodotto delle soluzioni, dobbiamo moltiplicare le loro formule.
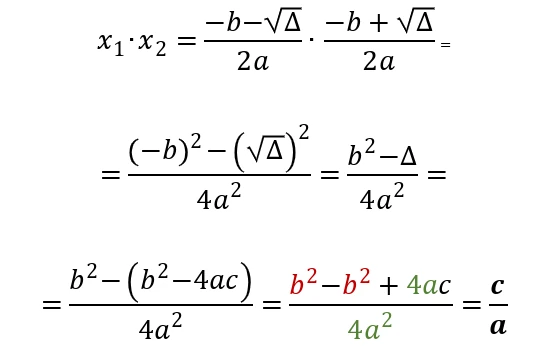
Riassumendo, la somma delle due soluzioni di un’equazione di secondo grado è uguale all’inverso del rapporto tra il coefficiente del termine di primo grado con quello del termine di secondo grado; il rapporto tra le due soluzioni è uguale al rapporto tra il termine noto e il coefficiente del termine di primo grado.
Somma e prodotto per risolvere le equazioni
Le equazioni di secondo grado ci permettono di ricavare due numeri conoscendo soltanto il valore della loro somma e del loro prodotto. Inoltre, possiamo semplificare ancora di più un’equazione ridotta in forma normale se tutti i termini sono divisibili per il coefficiente del termine di secondo grado.

Abbiamo indicato con le lettere s e p la somma e il prodotto delle due soluzioni. Se la somma è divisibile per 2 possiamo anche applicare la formula risolutiva ridotta.



