Il metodo di Cramer permette di calcolare immediatamente i valori di due incognite quando nel sistema ci sono due equazioni lineari ridotti in forma normale, cioè composti soltanto da un valore per ciascuna incognita e un solo termine noto. Questa regola prende il nome dal matematico svizzero che la formulò: Gabriel Cramer.
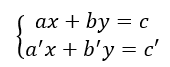
Riassumendo cosa sono i componenti di un’equazione, il coefficiente di un’incognita rappresenta valore numerico con cui viene moltiplicato quell’incognita mentre il termine noto rappresenta una parte numerica e non delle incognite. Un esempio di equazione è 3x – 2y = 5 che ci dice che la differenza tra il triplo dell’incognita x e il doppio di y è uguale a 5.
Vedi anche: Le equazioni
Secondo il metodo di Cramer, la prima incognita (di solito indicata con x) è uguale al rapporto tra:
- la differenza del prodotto del coefficiente del secondo membro della seconda equazione con il termine noto della prima equazione e il prodotto del coefficiente del secondo membro della prima equazione con il termine noto della seconda e
- la differenza tra il prodotto del coefficiente del primo membro della prima equazione con quello del secondo membro della seconda e il prodotto tra il coefficiente del primo membro della seconda equazione con quello del secondo membro della prima.

La seconda incognita (di solito indicata con y) è uguale al rapporto tra:
- la differenza del prodotto del coefficiente del primo membro della prima equazione con il termine noto della seconda equazione e il prodotto del coefficiente del primo membro della seconda equazione con il termine noto della prima equazione e
- la differenza tra il prodotto del coefficiente del primo membro della prima equazione con quello del secondo membro della seconda e il prodotto tra il coefficiente del primo membro della seconda equazione con quello del secondo membro della prima.

Dimostrazione del metodo di Cramer
Il metodo di Cramer si basa su quello di riduzione. Avendo due equazioni generiche ax + by = c e a’x + b’y = c’, dove a, b, a’ e b’ sono i coefficienti delle incognite mentre c e c’ sono i termini noti, si ricava la differenza tra membro a membro delle due equazioni e si sostituisce la nuova equazione ad una delle due equivalenti e si ricava prima la x e poi la y.

Abbiamo radunato i fattori comuni della x e quelli della y applicando la proprietà distributiva della moltiplicazione rispetto alla sottrazione. Da qui ricaviamo le incognite utili a risolvere il sistema:
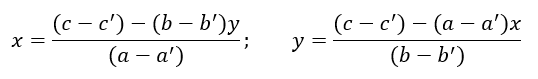
A questo punto possiamo ricavare le formule sostituendo a turno le nuove equazioni come mostrato nei prossimi paragrafi
Dimostrazione 1: ricaviamo la y
Si procede sostituendo la formula per ricavare la x ad una delle due equazioni del sistema:
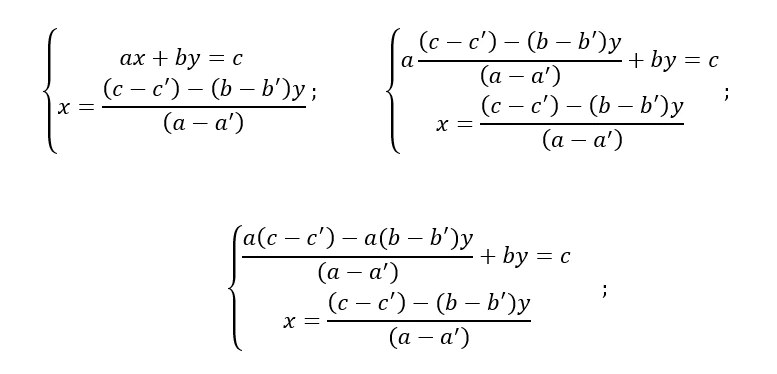
Nel prossimo passaggio applichiamo il secondo principio di equivalenza, moltiplicando tutti i membri della prima equazione per il denominatore di un membro, eliminando le frazioni.
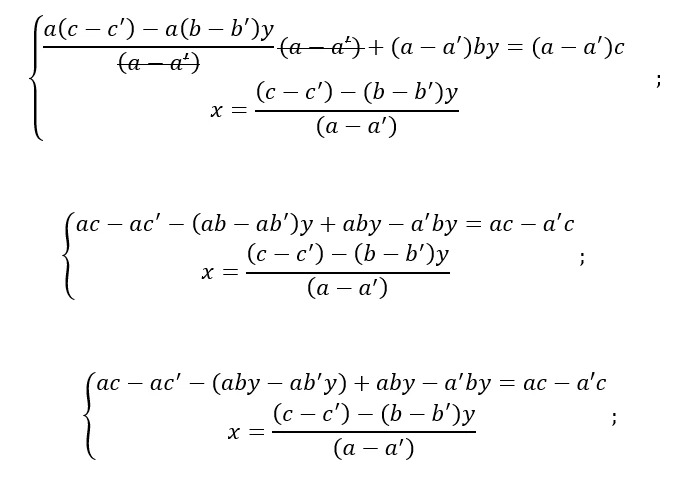
Applichiamo la regola dei segni e cancelliamo tutti i membri dell’equazione che sommandosi tra loro danno come risultato 0: -aby e +aby perché sono dalla stessa parte e si annullano mentre ac e ac perché se uno di loro si sposta nell’altra parte cambierebbe di segno e i due si annullerebbero.
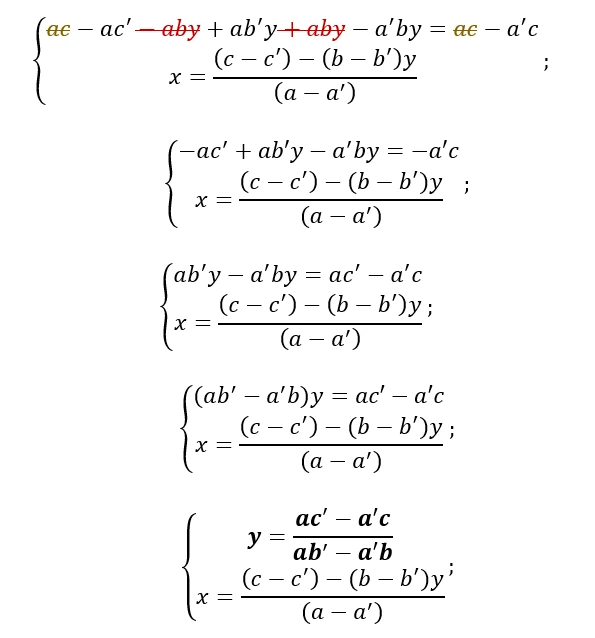
Dimostrazione 2: ricaviamo la x
Se applichiamo lo stesso metodo che abbiamo usato per ricavare la formula di y avremo come risultato la formula risolutiva della prima incognita:

Seguono i passaggi per ricavare la formula indicata sopra:
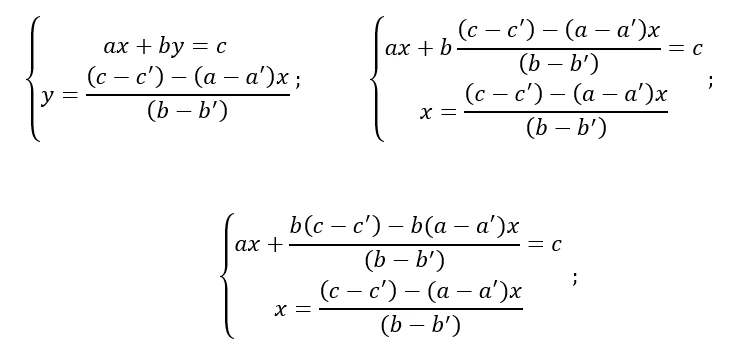
Nel prossimo passaggio applichiamo il secondo principio di equivalenza, moltiplicando tutti i membri della prima equazione per il denominatore di un membro, eliminando le frazioni.
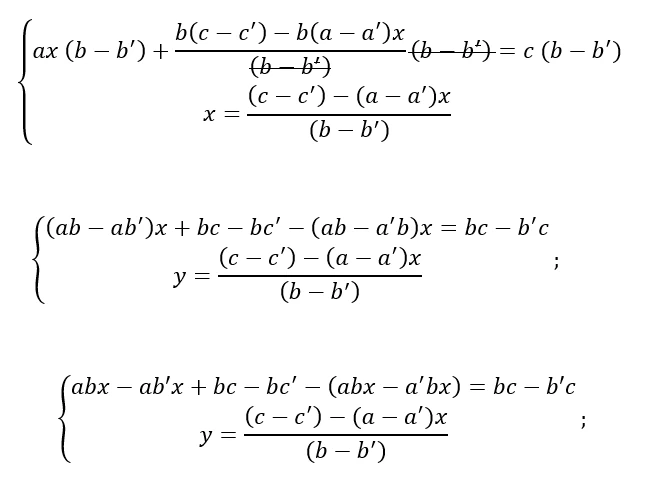
Applichiamo la regola dei segni e cancelliamo tutti i membri dell’equazione che sommandosi tra loro danno come risultato 0: -abx e +abx perché sono dalla stessa parte e si annullano mentre bc e bc perché se uno di loro si sposta nell’altra parte cambierebbe di segno e i due si annullerebbero.
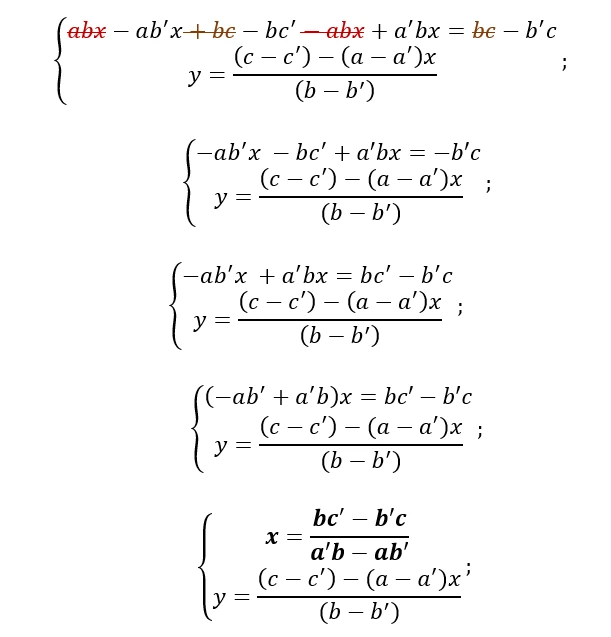
Tuttavia, preferiamo che al denominatore ci sia la stessa differenza usata per ricavare la seconda incognita mostrata nella dimostrazione precedente, sia per una sorta di comodità che per avere meno cose da dovere ricordare. Per fare ciò applichiamo al sistema iniziale della dimostrazione 2 il secondo principio di equivalenza, moltiplicando a ciascun membro di un’equazione un fattore letterale in modo da avere altre due equazioni equivalenti con un’incognita da potere annullare:

Semplificazione ed esempi del metodo di Cramer
Possiamo semplificare il metodo di Cramer chiamando determinante la differenza tra il prodotto dei coefficienti delle due incognite come mostrato sopra: D = ab’ – a’b. La determinante della prima incognita è uguale alla differenza tra il prodotto del primo coefficiente della seconda incognita con il secondo termine noto e il prodotto tra il secondo coefficiente con il primo termine noto: Dx = b’c – bc’. Per cui, la determinante della seconda incognita è uguale alla differenza tra il prodotto del primo coefficiente della prima incognita con il secondo termine noto e il prodotto tra il secondo coefficiente con il primo termine noto: Dy = ac’ – a’c. A questo punto le formule diventano:
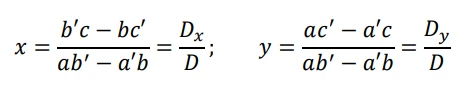
Come si può notare se il risultato della sottrazione al denominatore, cioè il dominante, risultasse 0 il sistema risulterà impossibile qualora uno degli altri dominanti è diverso da 0 oppure indeterminato nel caso in cui tutti i dominanti siano uguali a 0.
Proviamo a trovare le soluzioni comuni delle equazioni x + y = 5 e 2x – y = 2 con il metodo di Cramer: ricaviamo le tre determinanti riportando i coefficienti e i termini noti all’interno di alcune tabelle:
| ax | by |
|---|---|
| 1 | 1 |
| 2 | -1 |
D = -1 – 2 = – 3
| ax | c |
|---|---|
| 1 | 5 |
| 2 | 2 |
Dy = 2 – 10 = – 8
| by | c |
|---|---|
| 1 | 5 |
| -1 | 2 |
Dx = (-1) ∙ 5 – 1 ∙ 2 =
– 5 – 2 = -7
Infine, ricaviamo le incognite:
x = Dx / D = -7 / -3 = 7/3
y = Dy / D = -8 / -3 = 8/3



