Le equazioni binomie sono un tipo di equazione dove figura un polinomio con due termini, di cui una è un’incognita di qualsiasi grado. Per risolverle basta trovare il rapporto tra l’opposto del termine noto e il coefficiente dell’incognita e ricavare la radice elevata al grado dell’incognita.
Un’equazione binomia viene scritta generalmente nella forma axn + b = 0, dove la variabile b sta per il termine noto. Perciò, xn = – b/a e x = n√(-b/a). Valgono le stesse regole dei radicali, secondo cui le radici quadrate o con indice multiplo di 2 sono possibili soltanto se il radicando è positivo perché qualsiasi numero elevato ad una potenza con esponente pari è sempre positivo.
Se l’indice della radice è un numero dispari, la soluzione è soltanto una cioè la radice ennesima del rapporto tra l’opposto del termine noto e il coefficiente dell’incognita.
Dimostrazione ed esercizi sulle equazioni binomie.
Rivediamo un passo alla volta come si risolve un’equazione binomia:
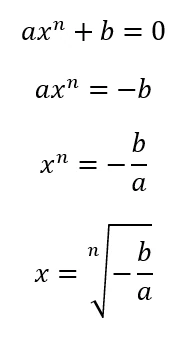
- Nel primo passaggio, abbiamo applicato il primo principio di equivalenza e spostato il termine noto al secondo membro cambiando il suo segno;
- Nel secondo passaggio abbiamo applicato il secondo principio di equivalenza, dividendo entrambi i membri dell’equazione per il coefficiente del termine incognito in modo da annullarlo al primo termine. Inoltre, abbiamo già fatto il rapporto dei segni della frazione per semplicità;
- Nel terzo passaggio abbiamo applicato di nuovo il secondo principio per rimuovere la potenza nell’incognita facendo la radice con in indice il suo esponente su entrambi i membri.
Proviamo a risolvere questa equazione: x3 – 27 = 0. In questo caso il coefficiente del termine incognito è 1 e viene sottinteso. La risoluzione è abbastanza semplice: x3 = 27; x = 3√27 = 3√33 = 3.
Risolvi questi esercizi e stabilisce se è possibile o impossibile:
2x5 + 64 = 0
3x4 + 243 = 0
3x3 + 9 ∙ 9 = 0



