L’esagono inscritto in una circonferenza è un poligono di sei lati i cui vertici toccano una circonferenza il cui raggio rappresenta la loro distanza dal suo centro.
Per costruire questo tipo di esagono su un foglio occorrono due squadrette, una da 45° e l’altra da 60°/30° e un compasso.
Disegniamo la nostra circonferenza con il centro O e un raggio qualsiasi e tracciamo gli assi ortogonali che passano dal centro. Puntiamo il compasso sul punto di intersezione dell’asse verticale con la circonferenza in basso e tracciamo un arco che ha lo stesso raggio del cerchio; facciamo la stessa cosa sul punto di intersezione sopra in modo da disegnare un arco che intersechi la circonferenza.

Il metodo per disegnare un esagono inscritto in una circonferenza è simile a quella del triangolo equilatero. In quel caso avevamo diviso la circonferenza in tre parti uguali, dove le tre corde corrispondevano ai tre lati del triangolo.
Vedi anche: Triangolo equilatero inscritto in una circonferenza
Questa volta uniamo i punti di intersezione dell’arco con gli estremi della circonferenza. Invece di unire i due punti di intersezione di ciascun arco, li uniamo al punto di intersezione più vicino tra l’asse verticale e la circonferenza ottenendo due archi che sono la metà di quello formato unendo i due punti dell’arco. La stessa cosa facciamo sopra, ottenendo così 4 archi uguali a 1/6 della circonferenza.
Anche le corde ottenute unendo i vertici rimanenti risultano uguali, di conseguenza anche i loro archi sono 1/6 della circonferenza data. Abbiamo ottenuto così un esagono regolare inscritto in una circonferenza.

Formule dell’esagono inscritto in una circonferenza
Guardando l’immagine sotto si può notare che il lato dell’esagono inscritto è uguale al raggio della circonferenza. Unendo gli estremi dell’esagono al centro del cerchio abbiamo disegnato 6 triangoli equilateri, con il lato che è uguale al raggio.
In questo modo, possiamo ricavare la formula dell’area del triangolo equilatero e dell’esagono: tracciando l’asse dal vertice di uno dei triangoli al lato opposto abbiamo ottenuto due triangoli rettangoli con la base uguale a metà del raggio.
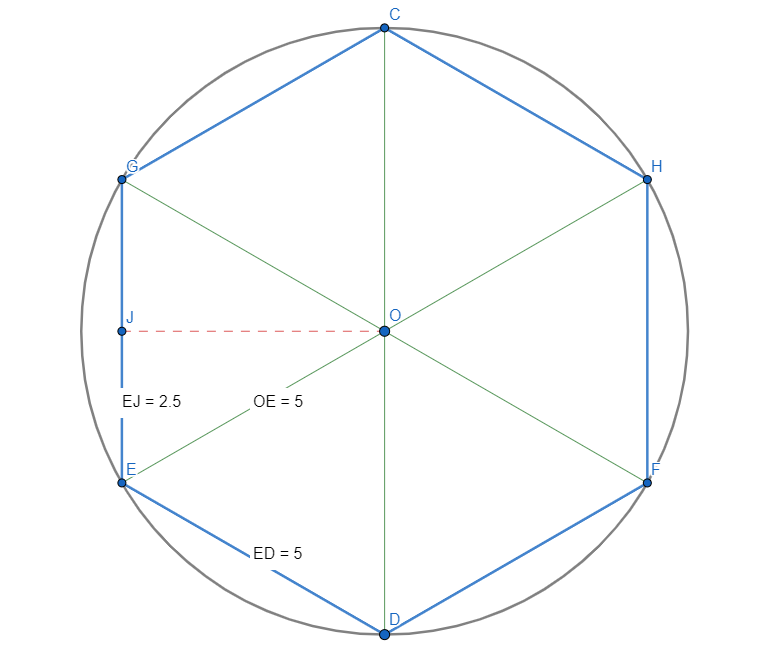
Ricaviamo l’altezza del triangolo equilatero mediante la formula inversa del teorema di Pitagora.

Trovata la formula dell’altezza, possiamo ricavare quella per trovare l’area di qualsiasi triangolo equilatero.

Per trovare l’area dell’esagono basterà moltiplicare l’area del triangolo per 6, che corrisponde al numero dei triangoli equilateri dentro l’esagono.

Abbiamo visto che disegnando un esagono inscritto in una circonferenza possiamo mediante ragionamento ricavare le formule per trovare la sua area; abbiamo anche trovato le formule per l’altezza e l’area di un triangolo equilatero.
Riassumiamo:




