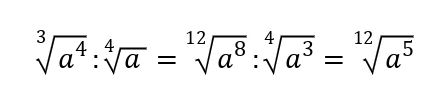La divisione tra due o più radici può essere fatta soltanto se tutti hanno lo stesso indice e il risultato sarà un radicale che ha lo stesso indice e il radicando uguale al quoziente dei radicandi. Se le radici hanno indici diversi si può ricorrere al minimo comune multiplo per ottenere radicali equivalenti ma con lo stesso indice e poi agire con la divisione.
I radicali sono un tipo di espressione matematica che viene indicata come un numero intero all’interno di una radice. Il numero racchiuso all’interno della radice viene chiamato radicando mentre il numero scritto in piccolo in alto a destra fuori della radice è il suo indice.
Per risolvere un radicale dobbiamo trovare quel numero che elevando sé stesso a una potenza che ha come esponente l’indice della radice ci fa ottenere il radicando. Quando non si può ottenere un numero intero, il radicale viene tenuto scritto così com’è proprio come fosse un monomio.
Come si fa la divisione tra radici
La definizione riguardante la moltiplicazione tra radici è la seguente: Il prodotto di due radicali con lo stesso indice e con radicando positivo o nullo è uguale a un radicale con lo stesso indice e con radicando il prodotto dei radicandi.
La dimostrazione avviene applicando la proprietà delle potenze su i singoli membri dell’equazione sotto:
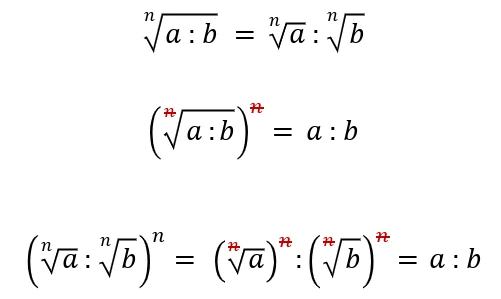
Lo stesso teorema vale anche per le frazioni:
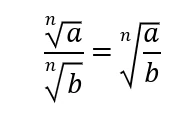
Per fare la divisione tra radicali con indici diversi dobbiamo ricavare il minimo comune multiplo (m.c.m.) dei loro indici, il quale diventerà il nuovo indice dei radicali. Per ricavare l’esponente dei radicandi dobbiamo applicare all’inverso la proprietà invariantiva, dividendo il m.c.m. con ciascun indice e moltiplicare il quoziente ottenuto con l’esponente del relativo radicando.