Le equazioni letterali sono delle uguaglianze scritte tra due espressioni algebriche dove, oltre alle lettere incognite il cui dobbiamo trovare i valori, ci sono altre lettere definite parametri che influenzano la veracità dell’equazione e che possono essere coefficienti delle incognite o rappresentare termini noti.
In generale, un’equazione è un’uguaglianza tra due espressioni algebriche il cui scopo è quello di ricavare il valore o la formula necessaria per trovare il termine incognito. Le equazioni già risolte, cioè ridotte in forma normale, come x = 2 e x = a + 2, permettono di conoscere il valore o l’insieme dei valori di x. Nella seconda equazione x dipende sempre da a ed è uguale aggiungendo 2 alla variabile a.
Per risolvere le equazioni letterali bisogna applicare gli stessi principi di equivalenza e le espressioni matematiche degli altri tipi di equazione. Ci sono casi, in cui alcun valori dei parametri rendano impossibile l’equazione, ad esempio quando questi sono coefficienti delle incognite oppure loro divisori. Ad esempio, in ax + 5 =6, se a è uguale a 0 l’equazione è impossibile come dimostra se si fanno i calcoli: 0 ∙ x + 5 = 6; 0 + 5 = 6 è impossibile. Perciò prima di risolvere l’equazione, scriviamo che se a = 0, l’equazione è impossibile.
Equazioni letterali intere
Sono la forma più semplice di questo tipo di equazioni e sono chiamate così quando l’incognita non si trova mai al denominatore di una frazione. Dopo avere ridotto l’equazione in forma normale si stabiliscono i casi in cui questa si dice:
- Determinata: Se la soluzione consiste in un numero limitato di valori
- Indeterminata: Se i valori che rendono vera l’equazione sono infiniti
- Impossibile: Quali valori la rendono impossibile.
Un esempio è a2x+2ax =15x – 3 + a, che può essere ridotto nella forma:
(a + 5)(a – 3)x = a – 3
A quel punto possiamo indicare quanto segue:
- Se a = -5 avremo 0 ∙ 2 ∙ x = – 5 – 3; 0 = – 8; Equazione impossibile
- Se a = 3 avremo 8 ∙ 0 ∙ x = 3 – 3; 0 = 0; Equazione impossibile
- Se a ≠ -5 e a ≠ 3, possiamo ricavare la formula dell’incognita
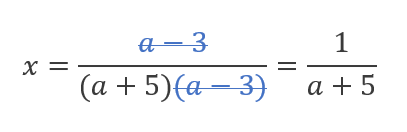
Equazioni letterali fratte
Nelle equazioni letterali fratte, una o più incognite compaiono al denominatore di una o più frazioni. In questo caso bisogna stabilire le condizioni di esistenza (C.E.), cioè quei valori delle lettere incognite per cui l’uguaglianza è sempre vera.
Si procede con le operazioni algebriche che permettono di rimuovere le incognite al denominatore, spesso sommando le frazioni, oppure applicando il secondo principio di equivalenza. Il procedimento è successivamente abbastanza semplice: si riportano i valori delle incognite da un lato e i termini noti dall’altro lato, si scompongono i polinomi e si ricavano le formule per calcolare il valore delle singole incognite.

In questo articolo c’è la spiegazione dell’esercizio. .



