I triangoli simili sono dei poligoni formati da tre lati che hanno gli angoli uguali: questo fa in modo che il rapporto tra i lati di un triangolo è sempre uguale anche nel caso in cui la loro lunghezza aumenta o diminuisce. Per questo motivo si dice che i loro lati sono in proporzione tra loro.
Che due triangoli siano simili lo si capisce anche quando quello più piccolo, sovrapponendo uno dei suoi vertici su quello corrispondente al triangolo più grande, ha due lati sovrapposti all’altro e il lato non sovrapposto è parallelo al lato più grande. Questa spiegazione è legata al fatto che le basi dei due triangoli possono essere considerate parti di rette parallele tagliata da due trasversali rappresentati dagli altri due lati. Per il teorema di Talete, i segmenti formati dall’intersezione di due rette parallele con due trasversali sono direttamente proporzionali tra loro: il loro rapporto è sempre uguale anche se aumentasse o diminuisse la distanza tra le parallele. Nell’immagine sotto è sottinteso che ci sia un’altra parallela sopra il vertice superiore.
Vedi anche: Le proporzioni
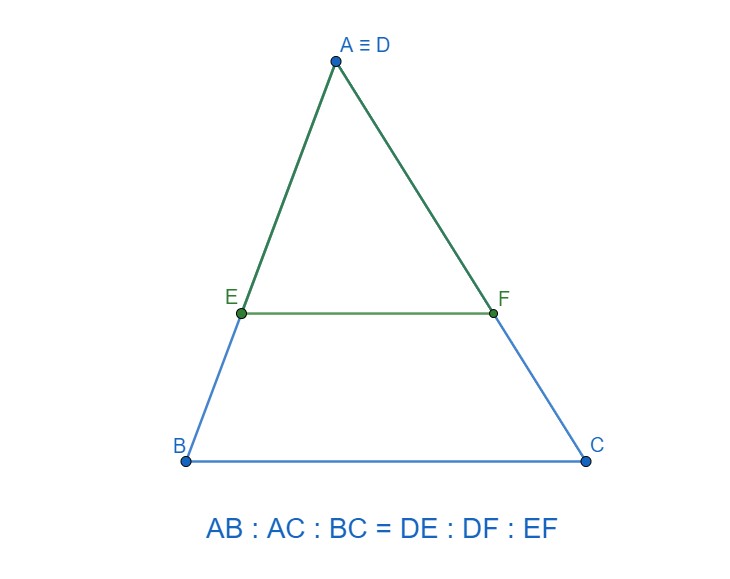
Nei problemi di geometria, questa proporzione ci permette di ricavare i lati di un secondo triangolo conoscendo la misura di un solo lato e dei lati del primo.
Criteri di similitudine
Come per i criteri di congruenza, i triangoli hanno anche dei criteri che ci permettono di stabilire se sono simili. Vediamo in breve quali sono i tre criteri di similitudine:
Il primo criterio dice che se due triangoli hanno due angoli ordinatamente della stessa ampiezza sono simili. Infatti, la somma degli angoli interni di un triangolo è sempre di 180°, perciò il terzo angolo del primo triangolo sarà congruente a quello del secondo, ricavati entrambi dalla differenza di angoli congruenti. I lati dei due triangoli saranno, perciò, in proporzione tra loro.
In base al secondo criterio, se due triangoli hanno due lati ordinatamente proporzionali tra loro e gli angoli compresi tra i lati congruenti, i due triangoli sono simili come conseguenza del teorema di Talete in quanto i due lati sono segmenti ricavati da due trasversali che tagliano delle parallele. Inoltre, possiamo affermare che due triangoli rettangoli che hanno i due cateti in proporzione sono simili;
Due triangoli sono simili se hanno tutti e tre i lati in proporzione, sempre come conseguenza del teorema di Talete perché sono considerati come segmenti ottenuti da parallele tagliate da due trasversali.
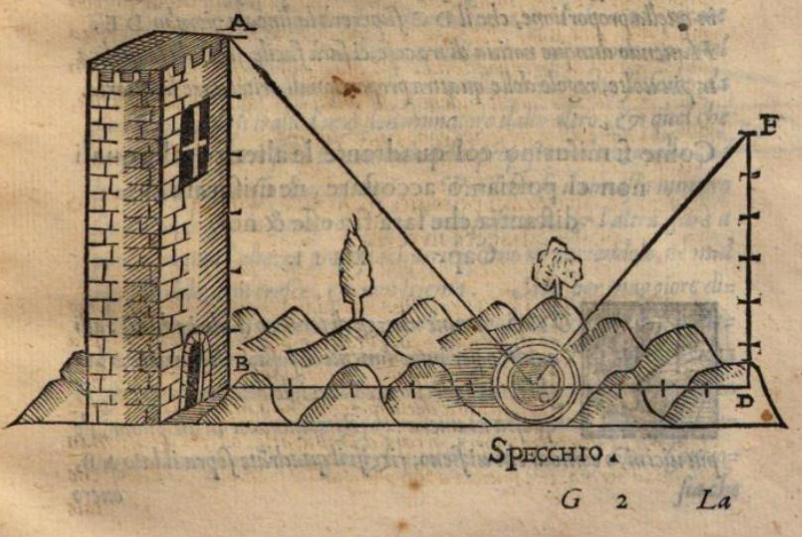
Già nel Cinquecento, il letterato fiorentino Cosimo Bartoli aveva applicato i criteri di similitudine e spiegato come calcolare l’altezza di un edificio servendosi di un semplice specchio. Nel suo libro Del modo di misurare, tra i vari metodi suggerì di porre uno specchio a terra ad una certa distanza dall’edificio e di allontanarsi dallo specchio fino a quando non si sarebbe visto l’edificio specchiato. Bisogna conoscere la propria altezza e la distanza dallo specchio sia rispetto l’edificio che rispetto l’osservatore. Gli angoli di riflessione della luce sullo specchio hanno la stessa ampiezza, perciò, è come se avessimo formato due triangoli rettangoli simili: il primo come cateti la distanza tra l’edificio e lo specchio e l’altezza dell’edificio, il secondo avente come cateti la distanza tra l’osservatore e lo specchio e l’altezza che parte da terra fino agli occhi dell’osservatore. Tramite una semplice proporzione, si sarebbe stati in grado di misurare l’altezza di un qualsiasi edificio.
Esercizi sui triangoli simili
- Il triangolo ABC, disegnato come nella figura sopra, ha il lato AB di 10,3 cm, il lato BC di 9 cm e il lato AC di 9,8 cm. Il triangolo DEF ha la base EF lunga 5 cm. Sapendo che i due triangoli hanno angoli uguali, ricava i lati mancanti del triangolo DEF.
- Se il rapporto tra i lati di due triangoli è costante e un angolo del primo triangolo è ampio 36°, quanto misura il rispettivo angolo del secondo triangolo?
- Disegna un triangolo e costruisci tre triangoli simi che hanno come rapporto di similitudine 2, 1/3 e 3.



