I vettori sono grandezze fisiche che non possono essere definite solo con un valore numerico e un’unità di misura. Per esempio, la velocità del vento non è solo una questione di quanto velocemente soffia, ma anche di dove soffia.
I vettori sono rappresentati graficamente da frecce, che indicano la direzione e il verso della grandezza.
In questo articolo, spiegheremo cosa sono i vettori, come si rappresentano graficamente e come si possono sommare, sottrarre e moltiplicare.
Cosa sono i vettori
In Fisica, i vettori sono delle grandezze rappresentate graficamente da una freccia con una direzione e un verso stabiliti. Questo perché alcune grandezze non si possono definire semplicemente indicando un valore numerico e un’unità di misura.
Per esempio, se vogliamo definire la velocità del vento, dobbiamo anche specificare la sua traiettoria. Anche quando si valutano le resistenze alle sollecitazioni di un edificio sono essenziali le grandezze vettoriali. Altri esempi sono le forze e i campi elettrici.
I vettori, chiamati anche grandezze vettoriali, hanno tre caratteristiche:
- Modulo o intensità, cioè la lunghezza della freccia che indica il valore numerico della grandezza fisica;
- Direzione, cioè la retta dove poggia la freccia che ne indica l’orientamento;
- Verso, che può andare da sinistra a destra o da destra verso sinistra.

In questo modo possiamo essere molto più precisi. Ad esempio, se stiamo viaggiando a 50 km/h possiamo dire anche quale strada stiamo percorrendo, da dove siamo partiti e dove stiamo andando.
Se un corpo subisce una forza, possiamo indicare in quale punto di questo corpo sta agendo la forza e in quale angolazione.
Il simbolo dei vettori può essere una lettera in grassetto o una lettera con sopra una freccia che ne indica il verso. Ad esempio, scriveremo V oppure ![]() . I vettori si possono sommare, sottrarre e moltiplicare.
. I vettori si possono sommare, sottrarre e moltiplicare.
Operazioni con i vettori
Ci sono diversi tipi di operazioni con i vettori. E’ possibile sommarli o sottrarli ad un altro vettore ed è anche possibile moltiplicarli ad un numero o scomporli.
Per sommare o sottrarre due o più vettori è possibile ricorrere al metodo punta-coda: si unisce la punta del primo vettore con la coda di quello successivo e si traccia un nuovo vettore che parte dalla coda del primo e arriva alla punta dell’ultimo vettore aggiunto.
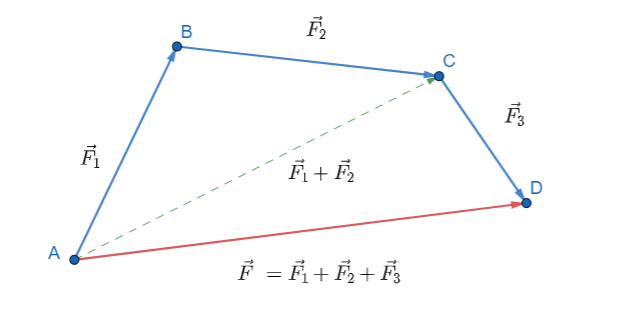
Nel caso in cui bisogna sottrarre due vettori, significa che il secondo ha direzione opposta al primo: basta perciò sommare il primo vettore con l’inverso del secondo.
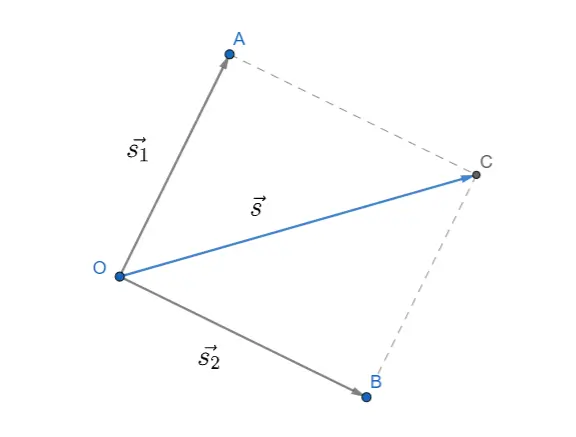
Se i vettori hanno la stessa origine possiamo applicare il metodo del parallelogramma: i due vettori rappresentano i lati mentre la loro somma è la diagonale del parallelogramma. Nel caso ci fosse un terzo vettore, questo si sommerà dopo con la somma dei primi due creando un nuovo parallelogramma.
Il prodotto scalare e vettoriale sono due operazioni matematiche che combinano due vettori per ottenere un risultato. Il prodotto scalare è un numero, mentre il prodotto vettoriale è un altro vettore. Per potere fare queste operazioni è necessario conoscere le funzioni goniometriche
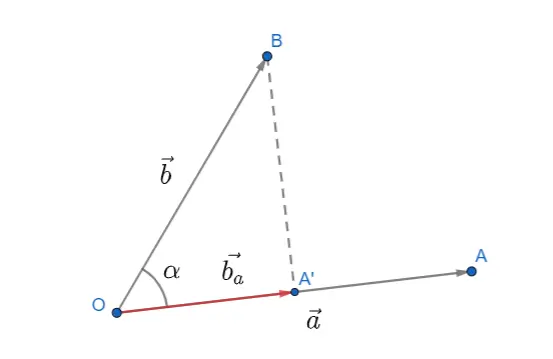
Il prodotto scalare è definito come il prodotto dei moduli dei due vettori per il coseno dell’angolo compreso tra di loro. In altre parole, ci dice quanto due vettori sono “allineati”.
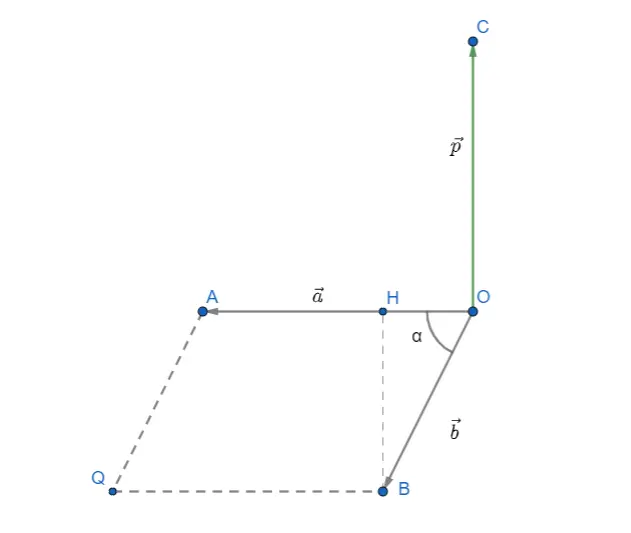
Il prodotto vettoriale è definito come un vettore che ha direzione perpendicolare al piano in cui poggiano i due vettori e il verso uscente immaginando di avere il palmo della mano destra appoggiato nel loro piano con il pollice in direzione del primo vettore e le altre dita orientate nella direzione del secondo vettore. Il modulo sarà uguale al prodotto dei due moduli con il seno dell’angolo compreso tra di loro.
Prova a rispondere a queste domande:
- Cos’è un vettore?
- Come si rappresenta graficamente?
Vedi anche: Le grandezze fisiche fondamentali del Sistema Internazionale
Applicazioni
La conoscenza dei vettori è fondamentale per costruire strutture solide e resistenti, prevenire disastri naturali e comprendere una vasta gamma di fenomeni fisici.
Il prodotto scalare e vettoriale hanno diverse applicazioni in fisica e ingegneria. Ad esempio, il prodotto scalare può essere utilizzato per calcolare il lavoro compiuto da una forza, mentre il prodotto vettoriale può essere utilizzato per calcolare il momento angolare di una particella.
Dalla progettazione di edifici e ponti allo studio del moto dei pianeti, i vettori sono uno strumento potente che ci permette di modellare e comprendere il mondo che ci circonda.
Le grandezze vettoriali sono inoltre fondamentali nello sviluppo dei videogiochi, soprattutto quando si tratta dello spostamento dei personaggi, lo spostamento della telecamera, la fisica del gioco come l’aggiunta della gravità e le animazioni.
