Le proprietà delle potenze con le frazioni sono le stesse regole che si studiano e si applicano per le potenze dei numeri naturali e sono il prodotto di potenze che hanno la stessa base o lo stesso esponente, il quoziente di potenze che hanno la stessa base o lo stesso esponente e la potenza di potenza. Questo ci permette di definire anche le potenze con frazioni elevate a 1 e a 0 proprio come per i numeri naturali.
Il prodotto di potenze che hanno la stessa base è uguale ad un’altra potenza che ha la stessa base ma come esponente la somma degli esponenti delle potenze da moltiplicare.

Per risolvere il quoziente di potenze che hanno la stessa base basterà scrivere un’altra potenza che ha sempre la stessa base e sottrarre il secondo esponente al primo.
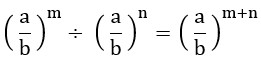
La stessa cosa vale per il prodotto e il quoziente di potenze che hanno lo stesso esponente. In questo caso la potenza con la frazione risultante avrà sempre lo stesso esponente ma come base avrà la somma delle frazioni che sono le basi delle varie potenze. Questo significa trovare il minimo comune multiplo dei denominatori, dividerlo per i denominatori e moltiplicare quoziente ottenuto con i rispettivi denominatori. A quel punto basterà sommare o sottrarre i vari risultati ottenuti.

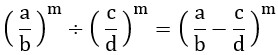
- Vedi anche Le addizioni tra frazioni e Le sottrazioni tra frazioni
Per risolvere la potenze di una potenza con all’interno una frazione si opererà allo stesso modo dei numeri interi: la base della potenza risultante avrà la stessa base di quella iniziale e avrà come esponente il prodotto degli esponenti della potenza iniziale.

Grazie alla seconda proprietà delle potenze possiamo definire anche le potenze con le frazioni elevate a 1 e a 0. In questo caso tutte le potenze elevate a 1 equivalgono allo stesso numero senza esponente, in altre parole la base si può scrivere senza esponente.
Quando una potenza viene elevata a 0 è come se stessimo dividendo una potenza per se stessa. Infatti se applichiamo la seconda proprietà abbiamo:
am : am = am-m = a0 ; am : am = 1
Quindi, qualsiasi potenza elevata a 0, compresa quella che contiene delle frazioni, equivale a 1.

Nel caso in cui una potenza ha l’esponente negativo, la si può convertire in un’altra potenza che ha l’esponente di segno positivo ma con il numeratore al posto del denominatore e viceversa. Sotto possiamo vedere una dimostrazione generica di una potenza con esponente negativo ricavata dividendo due potenze con la stessa base in due modi diversi.

Nel primo caso si è ricavato il risultato delle singole potenze e tramite una semplificazione si è ricavata la potenza risultante positiva.
Nel secondo caso è stata applicata la seconda proprietà delle potenze; si può notare che i due risultati devono dare lo stesso valore e perciò vale la definizione sopra. E’ possibile giungere la stessa conclusione usando valori diversi.



