Per trasformare un numero periodico in una frazione basta inserire al numeratore la differenza tra tutto il numero decimale senza la virgola e il numero formato dalle cifre non periodiche; per il denominatore bisogna contare quante sono le cifre non periodiche e scrivere altrettanti 9 e poi bisogna contare quante sono le cifre decimali non periodiche e scrivere altrettanti 0. Nei prossimi paragrafi viene spiegato e dimostrato questo metodo.
Un numero periodico è un numero decimale, cioè che contiene una parte decimale che segue la parte intera dopo la virgola, che ha una o un gruppo di cifre che si ripete all’infinito, per sempre. Questo gruppo di cifre viene chiamato periodo mentre le cifre decimali che appaiono soltanto una volta costituiscono l’antiperiodo.
La frazione è invece una divisione tra due numeri scritti uno sopra l’altro e divisi da una linea retta: il dividendo viene scritto sopra e viene chiamato numeratore mentre il divisore viene scritto sotto e viene chiamato denominatore. La frazione in cui il rapporto tra numeratore e denominatore dà il numero decimale periodico interessato viene chiamata frazione generatrice.
Vediamo adesso un esempio che ci dimostra come convertire un numero periodico in frazione. Proviamo a trasformare 1,27365 (le cifre in grassetto rappresentano la parte periodica). Scriviamo un’equazione e stabiliamo che la lettera a è uguale al numero periodico interessato.
a = 1,27365
Innanzitutto spostiamo la virgola del numero decimale alla fine dell’antiperiodo. In questo caso, dobbiamo moltiplicarlo per 100 e facciamo la stessa cosa per a, scrivendolo sottoforma di potenza del 10.
102a = 127,365
Spostiamo la virgola del numero decimale alla fine del primo gruppo di cifre periodiche. Per farlo bisogna moltiplicarlo per 1000 e facciamo la stessa cosa con la lettera a.
103 ∙ 102a = 127365,365
Troviamo adesso la differenza tra l’ultimo risultato ottenuto e il primo.
103 ∙ 102a – 102a = 127365,365 – 127,365
Nella parte numerica dell’equazione possiamo applicare la proprietà invariantiva della sottrazione togliendo ad entrambi i numeri periodici la parte decimale.
103 ∙ 102a – 102a = 127365 – 127
Nella parte algebrica dell’equazione applichiamo la proprietà distributiva della moltiplicazione rispetto alla sottrazione ed estrapoliamo 102a.
(103 – 1) ∙ 102a = 127365 – 127
Risolviamo prima la parte algebrica e ricaviamo la formula per trasformare questo numero periodico in frazione
(1000 – 1) ∙ 102a = 127365 – 127
999 ∙ 100a = 127365 – 127
99900a = 127365 – 127
Applicando il secondo principio di equivalenza è facile ricavare la frazione generatrice di questo numero periodico. Possiamo notare che al numeratore c’è davvero la differenza tra il numero senza virgola e la sua parte periodica considerata come intero al numeratore e al denominatore ci sono tanti 9 quante le cifre del periodo e tanti 9 quante le cifre dell’antiperiodo. Dopo avere risolto la differenza al numeratore basterà fare una semplificazione.
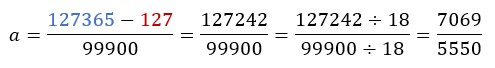
Prova adesso a trasformare i seguenti numeri periodici in frazioni tenendo presente che se non ci sono cifre non periodiche non si aggiungono zeri: 0,6; 1,6; 0,1; 0,5; 0,083; 0,5; 0,3; 0,45679; 46,245.



