Due angoli complementari sono due parti di un piano delimitati da due semirette che hanno un lato e il vertice in comune e gli altri due lati sono disposti in modo che la somma delle loro due ampiezza dia come risultato un angolo di 90°, un angolo retto. Nel sistema di misura centesimale la loro somma equivale a 100c mentre in radianti è uguale a π.
Nella figura sono stati disegnati i angoli α (DAC) e β (CAB): questi sono complementari perché la loro somma equivale ad un angolo retto, 90 gradi, come si intuisce guardano l’angolo più grande che li copre entrambi. I due angoli, inoltre, devono essere per forza acuti, cioè devono avere la forma appuntita, aguzza, essendo entrambi minori di 90°.
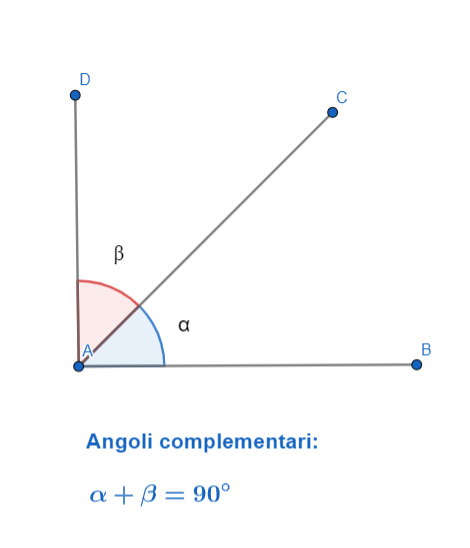
Nell’immagine vista sopra, i due angoli sono anche consecutivi ma non è obbligatorio che sia sempre così. In un triangolo rettangolo, per esempio, i due angoli acuti sono uno il complementare dell’altro. Sapendo che la somma degli angoli interni di un triangolo è sempre di 180° e l’angolo opposto all’ipotenusa di un triangolo rettangolo è di 90°, ne deriva che la somma degli altri due angoli è uguale a 180 – 90 gradi.
Problemi con gli angoli complementari
Quanto misura un angolo sapendo che sommato con un altro di 70° dà un angolo retto?
In questo caso ci basterà sottrarre all’angolo retto il secondo angolo. Quindi scriveremo:
α = 90° – β = 90° – 70° = 20°
Prova a risolvere questi esercizi:
- Due angoli misurano rispettivamente 15° e 75°. Sono complementari?
- Un angolo di 57°30′ è complementare con un altro angolo di misura ignota. Ricavare il valore del secondo angolo. (Per risolvere questo problema bisogna sapere fare le operazioni con il sistema sessagesimale)
- Abbiamo due angoli la cui somma è un angolo piatto. Se il primo misura 40c, quanto è ampio il secondo angolo? (Per risolvere questo esercizio bisogna conoscere il sistema centesimale).
Vediamo un altro esempio: Ricaviamo il valore di due angoli complementari sapendo che uno è il doppio dell’altro.
Per risolvere questo problema dobbiamo capire il testo. Leggendolo capiamo che il secondo angolo è il doppio del primo e che la loro somma dà 90 gradi. Useremo una semplice equazione per risolverlo:
x + 2x = 90°
3x = 90°
α = x = 90° /3 = 30°
β = 2α = 2 ∙ 30° = 60°
Abbiamo così trovato il valore dei due angoli. Infatti, 30° + 60° = 90°. Quanto misurerebbero i due angoli se il secondo fosse il triplo del primo? Sapresti risolvere questo esercizio usando i sistemi lineari a due incognite?



