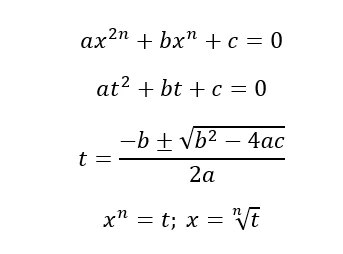Le equazioni

Le equazioni sono la forma scritta di uguaglianze fra due espressioni letterali dove una o più lettere, chiamate incognite, hanno dei valori specifici che rendono vera un’uguaglianza. Lo scopo è quello di ricavare i valori delle incognite.

Un equazione viene scritta mettendo a confronto due espressioni letterali come 3x + 2 = 4x -1. In questo caso l’incognita da trovare e x, cioè il valore che sostituito a questa lettera fa avere lo stesso risultato sia all’espressione che si trova a sinistra sia all’espressione che si trova nella destra del segno di uguaglianza.

Esistono uguaglianze tra espressioni letterali che sono sempre vere a prescindere dal valore che viene attribuito alle lettere. Un esempio è il quadrato di un binomio la cui uguaglianza si può scrivere:

(A + B)(A + B) = A² + 2AB + B²

Infatti, risolvendo l’espressione a sinistra si otterrà la stessa formula di quella a destra. Questo tipo di uguaglianza non viene chiamate equazione ma identità perché è valida sempre.

Classificazione delle equazioni

Le equazioni possono essere classificate in algebriche o trascendenti. Nel primo caso, nelle espressioni messe a confronto appaiono soltanto polinomi o frazioni algebriche. Inoltre, un’equazione algebrica può essere anche intera se le incognite sono al numeratore oppure fratta, o frazionaria, quando le incognite appaiono al denominatore.

Un’equazione può essere classificata anche in base alle lettere presenti. Nel caso in cui appaiono soltanto le incognite come lettere, allora l’equazione viene chiamata numerica. Se oltre alle incognite ci sono altri tipi di lettere, l’equazione viene chiamata letterale e le lettere sono dette parametri.

• 3x – 4 = x è numerica;
• 9x + a = 5a è letterale nell’incognita x se a è un parametro.

Nei problemi di geometria i valori che abbiamo già a disposizione sono i parametri mentre il valore da ricavare è l’incognita. Se di un rettangolo conosciamo l’area e l’altezza e dobbiamo ricavare la base, le prime due grandezze sono i parametri e la base è l’incognita. A = x ∙ h, dove x = b.

Infine, le equazioni possono essere classificate in base al numero di soluzioni. Se questa hanno un numero finito l’equazione si dice determinata, se hanno un numero infinito di valori che rendono l’uguaglianza vera l’equazione è indeterminata mentre se non ci sono soluzioni viene chiamata impossibile.

• 4x + 3x = 7x è indeterminata perché è vera a prescindere dal valore di x ed è anche un’identità.

Princìpi di equivalenza

Due equazioni con le stesse incognite che hanno le medesime soluzioni sono dette equivalenti come ad esempio x + 4 = 7 e 3x = 9.

• x = 7 – 4 = 3
• x = 9/3 = 3

Possiamo passare da un’equazione complessa ad una equivalente più semplice applicando i princìpi di equivalenza che si basano sulle leggi delle uguaglianze fra numeri.

Il primo principio di equivalenza stabilisce che se aggiungiamo o togliamo a entrambi i membri di un’equazione uno stesso termine otteniamo un’equazione equivalente.

Spesso è utile per fare in modo di non avere incognite nel membro dell’equazione a destra, come nell’esempio sotto:

3x + 4 = 4x + 2

3x + 4 – 4x = 4x + 2 – 4x

3x + 4 – 4x = 2

Come possiamo vedere, l’incognita a destra si annulla con il suo opposto, dato che 4x – 4x = 0. E’ come se avessimo spostato il monomio con l’incognita nell’espressione a sinistra e lo avessimo cambiato di segno. Facendo la somma algebrica anche a sinistra avremo:

3x + 4 – 4x = 2

– x + 4 = 2

Adesso, però, x è negativo. Come facciamo a risolvere l’espressione? Applicando il secondo principio di equivalenza secondo cui se moltiplichiamo o dividiamo entrambi i membri di un’equazione per uno stesso numero o espressione letterale otteniamo un suo equivalente.

In questo caso moltiplichiamo tutti i membri con -1.

-1 ∙ (- x + 4) = -1 ∙ 2

x – 4 = – 2

Nel primo membro abbiamo moltiplicato -1 con ogni termine dell’espressione proprio come stabilito dalla proprietà distributiva. Abbiamo anche applicato la regola dei segni: il prodotto tra due segni uguali è sempre di segno positivo mentre da due segni diversi è sempre negativo.

Per continuare, applichiamo di nuovo il primo principio di equivalenza e spostiamo -4 a destra cambiandolo di segno. Questo passaggio viene chiamato regola del trasporto.

x – 4 = – 2

x = – 2 + 4

x = 2

Equazioni di secondo grado

Finora abbiamo visto equazioni dove l’incognita non viene espressa sotto forma di potenza ma capita spesso di dovere risolvere esercizi più complessi. Un’equazione dove l’incognita viene espressa con una potenza al quadrato viene chiamata di secondo grado.

In questo caso l’equazione viene scritta così: ax² + bx + c = 0, ax² + bx = 0 oppure ax² + c = 0. Nel primo caso si parla di equazioni di secondo grado complete e per risolvere bisogna utilizzare la formula risolutiva; per gli altri due casi basterà applicare i principi di equivalenza per ricavare la soluzione.

Risolvere le equazioni di grado superiore al secondo

E’ possibile risolvere le equazioni più complesse rispetto a quelle di secondo grado semplificandole, riportando tutti i termini dalla stessa parte trasformando l’equazione in un unico polinomio e scomponendolo in fattori; l’incognita apparirà più volte con gradi inferiori rispetto a prima e sarà possibile estrapolare le varie espressioni algebriche per ricavare i possibili valori dell’incognita.

Ad esempio, proviamo a risolvere x³ + 10 = -x effettuando i vari passaggi:

x³ +10 + x = 0

x³ + x + 10 = 0

x³ – 4x + 5x + 10 = 0

Abbiamo scomposto x con un’espressione equivalente per semplificare i prossimi passaggi:

x (x² – 4) + 5 (x + 2) = 0

x (x – 2) (x+2) + 5 (x + 2) = 0

(x+2) [x (x – 2) + 5] = 0

(x+2) (x² – 2x + 5) = 0

Si prendono le singole espressioni per ricavare i possibili valori dell’incognita

Ci sono altri tipi di equazione che seppur sono superiori al secondo grado, risultano più facili da risolvere:

Le equazioni binomie, sono formate soltanto da due termini e l’incognita è presente in qualsiasi grado. Si presentano nella forma axⁿ + b = 0 e per risolverle basta applicare i principi di equivalenza:

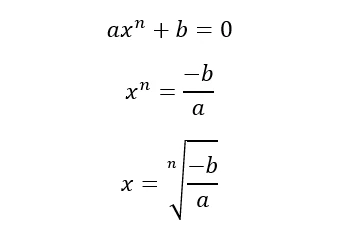
Le equazioni trinomie sono sempre complete ma l’incognita del primo termine è il quadrato di quella del secondo termine. Si presentano nella forma ax²ⁿ + bxⁿ + c = 0 e basta convertirle in un’equazione di secondo grado per poterle risolvere.