La parabola è una figura geometrica i cui punti hanno la stessa distanza da un punto fisso chiamato fuoco e da una retta, interna od esterna, chiamata direttrice. Questa figura riveste molta importanza sia nell’ingegneria che nell’architettura e nella fisica.
Nelle sue pubblicazioni, Galileo Galilei scrisse che quando un corpo viene lanciato nell’aria in assenza di attrito e con direzione parallela al suolo percorre una traiettoria parabolica. Quest’affermazione venne dimostata nel Settecento dal matematico e fisico Willem’s Gravesande.
In un piano cartesiano, la parabola rappresenta graficamente una funzione di proporzionalità quadratica, dove il rapporto tra la grandezza da ricavare e il quadrato della sua controimmagine è sempre costante, non varia neppure quando varia il valore delle due grandezze. La funzione di una proporzionalità quadratica nel piano cartesiano viene indicata così: y = a ∙ x2. Anche altre equazioni possono essere rappresentate da parabole.
– Vedi anche: Le funzioni
Parabola nel piano cartesiano
Il piano cartesiano è un sistema di riferimento formato da un asse verticale, chiamato ordinata, e un asse orizzontale, chiamato ascissa, che servono a ricavare la posizione dei punti al suo interno. Su ciascun asse viene inserita una linea graduata che rappresenta la distanza di ogni punto rispetto a tale asse.
E’ possibile vedere la rappresentazione grafica di una parabola utilizzando un qualsiasi programma di matematica o su un foglio. Dopo avere stabilito il valore della costante basterà trovare alcuni valori dell’ordinata dopo avere scelto il valore dell’ascissa. Ad esempio, nell’equazione y = 2x2 l’immagine della funzione sarà sempre uguale al doppio del quadrato della sua controimmagine.
| y | x |
|---|---|
| 32 | -4 |
| 16 | -2 |
| 0 | 0 |
| 16 | 2 |
| 32 | 4 |
Possiamo notare che il segno dell’immagine della funzione dipende dal segno della costante, in quanto il quadrato della controimmagine è sempre positiva.
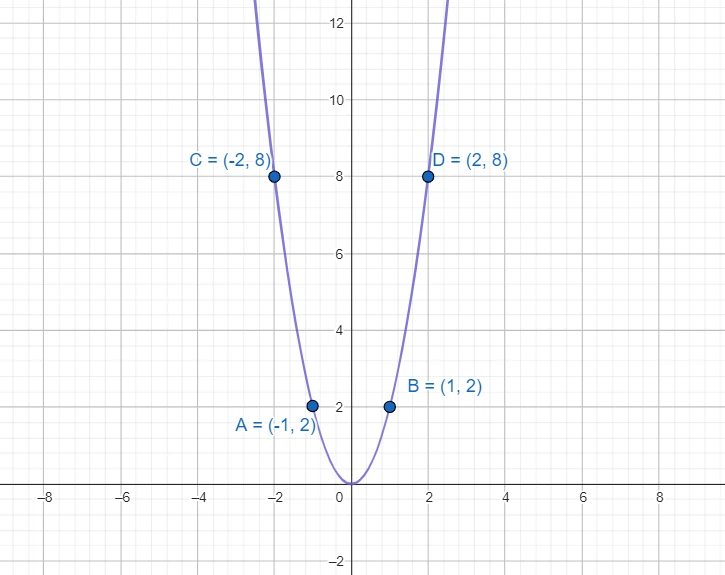
Prova tu: Disegna il grafico di una funzione y = -1/3x2
Il grafico di un’equazione di secondo grado competa y = ax2 + bx + c è sempre una parabola la cui ampiezza, pendenza e distanza rispetto l’asse orizzontale varia rispettivamente al variare del parametro del quadrato di x, del parametro dell’incognita e del termine noto.
Se il parametro del quadrato dell’incognita è maggiore di 0, la sua concavità è verso l’alto e la sua apertura aumenta all’aumentare del parametro; se è minore di 0, la concavità della parabola è rivolta verso il basso e la sua apertura aumenterà al diminuire del suo parametro. Nel caso il parametro fosse uguale a 0, l’equazione diventerebbe lineare e il grafico sarebbe una retta con equazione y = bx + c. In ogni caso la retta e le parabole toccherebbero l’asse delle ordinate sempre nello stesso punto.
Man mano che diminuisce il valore del parametro dell’incognita di primo grado, la pendenza della retta vista sopra diminuisce fino a quando diventa orizzontale nel momento che il valore del parametro è uguale a 0 e l’equazione diventa y = ax2 + c. Il vertice della parabola coinciderà con il punto di incontro con l’asse verticale che diventerà il suo asse di simmetria.
Il termine noto rappresenta il punto di intersezione tra la parabola e l’asse delle ordinate. In questa attività è possibile provare a modificare i parametri di un’equazione di secondo grado e vedere come cambia la parabola.
Costruzione di una parabola
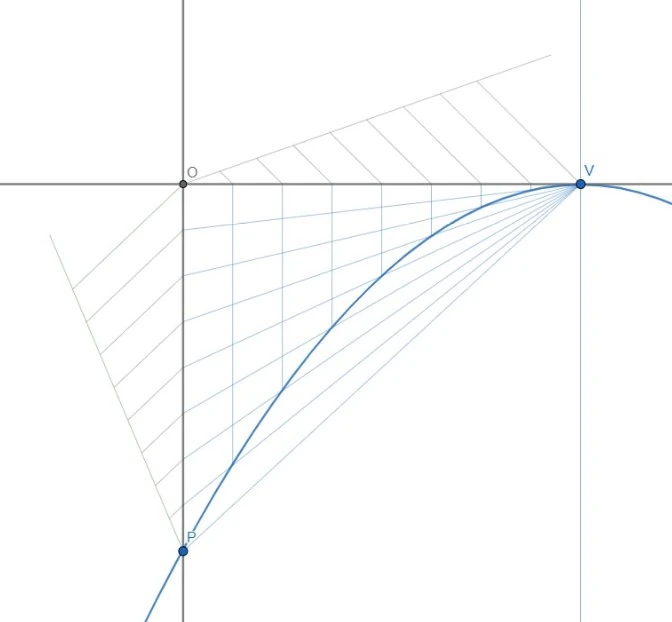
Per costruire una parabola dobbiamo avere già fissato il suo vertice, l’asse verticale e il punto di intersezione tra la parabola e l’asse.
Tracciamo la perpendicolare all’asse passante per il vertice e dividiamo i segmenti formati dal vertice e dal punto di intersezione con l’origine delle due perpendicolari in parti uguali.
Congiungiamo il punto di intersezione tra la parabola e l’asse con il vertice e tracciamo le parallele al loro segmento sui punti che dividono il segmento formato prima. Dopo avere diviso il segmento con estremi il vertice e l’origine degli assi tracciamo le perpendicolari a quel segmento sui punti trovati. I punti di intersezione tra le parallele del segmento con estremi il vertice e il punto e le perpendicolari sono i punti della parabola.
L’equazione di una parabola
Andiamo più in profondità e vediamo come si ricava l’equazione di una parabola con in vertice nell’origine del piano cartesiano e il suo asse coincidente l’asse delle ordinate. La direttrice è sempre perpendicolare all’asse della parabola e in questo caso è parallela all’asse delle ascisse; il fuoco è un punto che giace sull’asse y e che supponiamo distinto dall’origine degli assi. Le coordinate del fuoco saranno 0 e la sua distanza dall’asse delle ascisse, che indichiamo con yF.
Dato che tutti i punti di una parabola hanno la stessa distanza sia dal fuoco che dalla direttrice, il punto di intersezione tra l’asse della parabola con l’asse x avrà come coordinate 0 e l’opposto dell’ordinata del fuoco, cioè -yf. Dato che la direttrice è parallela all’asse delle ascisse, la sua equazione sarà semplicemente y = –yF.
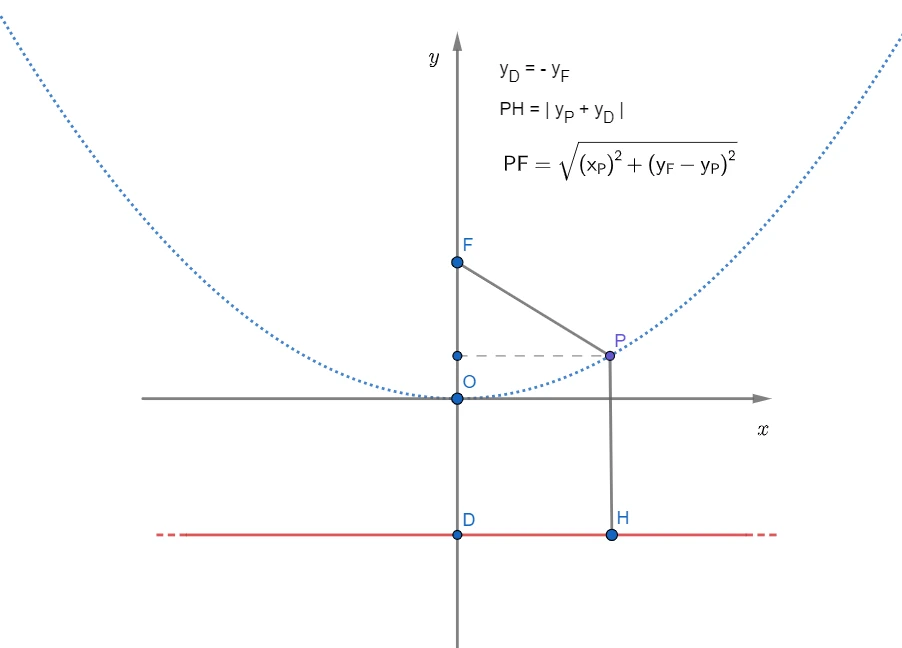
Qualsiasi punto della parabola avrà la distanza dalla direttrice uguale alla somma della sua ordinata e quella della direttrice mentre la sua distanza dal fuoco si ricava applicando il teorema di Pitagora sul triangolo che forma con la sua proiezione sull’asse delle ordinate e calcolando la radice quadrata tra la somma del quadrato della sua ascissa e il quadrato della differenza tra l’ordinata del fuoco e l’ordinata del punto interessato. A questo punto possiamo uguagliare le due espressioni per ricavare l’equazione della parabola, elevando entrambi i membri al quadrato per togliere la radice quadrata, applicando il quadrato di un binomio ed eliminando i termini opposti:
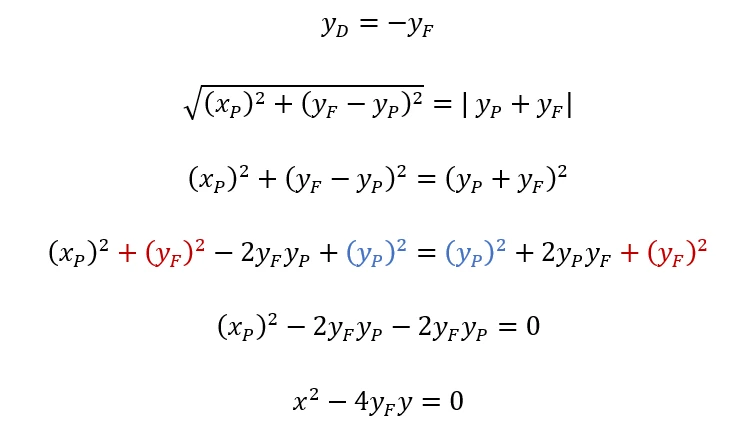
A questo punto possiamo ricavare l’equazione della parabola, l’ordinata del fuoco e l’equazione della direttrice.
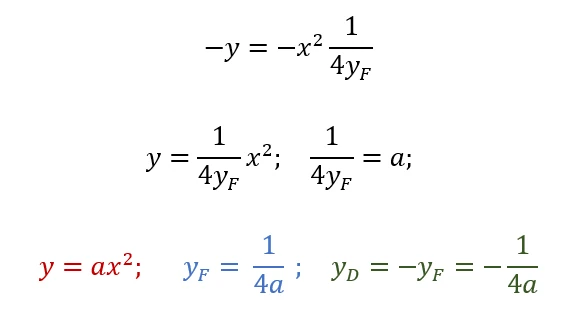
Parabole che non hanno il vertice sull’origine
Che dire di tutte le parabole che non hanno il vertice coincidente l’origine degli assi cartesiani? Proprio come nel caso delle rette parallele a quella passante per l’origine, anche in questo caso bisogna prendere come riferimento la parabola con il vertine sull’origine. In questo caso stiamo considerando quella che ha l’asse parallelo all’asse y.
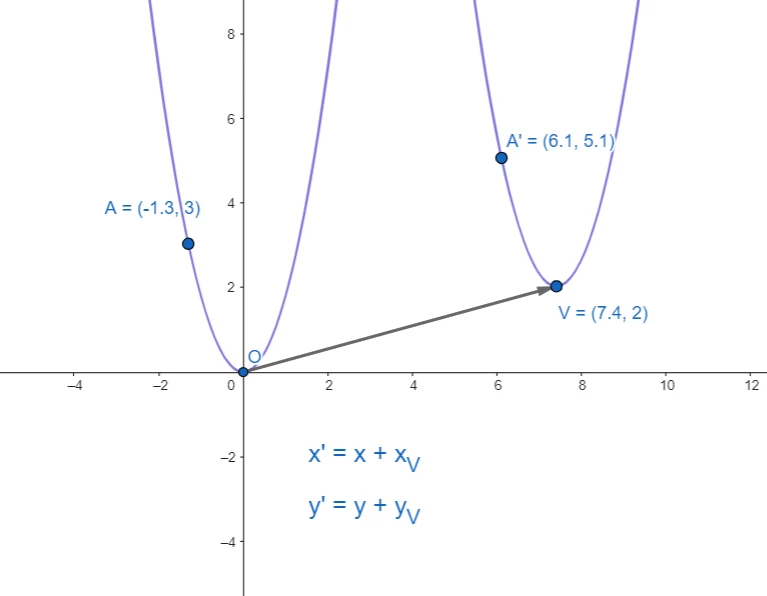
Si può notare dall’immagine che le coordinate dei punti di questa parabola si ricavano facendo la somma algebrica tra le coordinate dei punti della parabola con il vertice sull’origine degli assi cartesiani e le coordinate del vertice della parabola parallela ad essa. Possiamo uguagliare l’espressione per ricavare l’ordinata mostrata qui con quella ricavata prima e ricavare l’equazione della parabola con asse parallelo all’asse y.
y – yv = ax2
y – yv = a(x – xv)2
y – yv = a(x2 – 2xvx + x2v)
y – yv = ax2 – 2axvx + ax2v
y = ax2 – 2axvx + ax2v + yv
Stabiliamo di dare questi nomi ai valori trovati: – 2axv = b e ax2v + yv = c. Da qui derivano le varie formule ed equazioni:
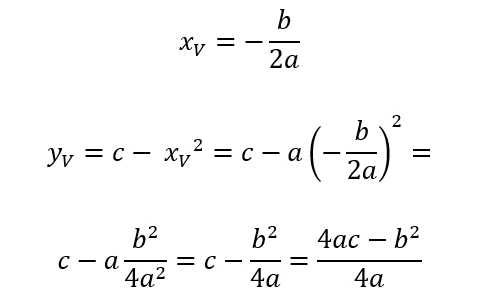
Nelle equazioni di secondo grado all’espressione b2 – 4ac viene assegnato il simbolo Δ per abbreviare. Nella formula sopra diventa – Δ, dato che i monomi hanno segno opposto al solito.
Riassumendo:
- L’equazione di una parabola con asse parallelo quello delle ordinate è un’equazione di secondo grado completa: y = ax2 + bx + c con il coefficiente dell’incognita di secondo grado diverso da 0;
- L’ascissa del vertice si ricava dall’opposto del rapporto tra il coefficiente dell’incognita di primo grado e il doppio del coefficiente dell’incognita di secondo grado, – b/2a;
- L’ordinata del vertice si ricava facendo il rapporto tra la differenza del quadruplo prodotto tra il coefficiente dell’incognita di secondo grado e il quadrato del coefficiente dell’incognita di secondo grado con il quadruplo del coefficiente dell’incognita di secondo grado, – Δ/4a.
Parabola con asse parallelo all’asse x
Nel caso in cui l’asse della parabola fosse parallelo all’asse delle ascisse valgono le stesse considerazioni fatto sopra con la differenza che in questo caso i termini da ricavare si invertono:
- L’equazione di secondo grado diventa x = ay2 + by + c con il coefficiente dell’incognita di secondo grado diverso da 0;
- L’ascissa del vertice si ricava facendo il rapporto tra la differenza del quadruplo prodotto tra il coefficiente dell’incognita di secondo grado e il quadrato del coefficiente dell’incognita di secondo grado con il quadruplo del coefficiente dell’incognita di secondo grado, – Δ/4a;
- L’ordinata del vertice si ricava dall’opposto del rapporto tra il coefficiente dell’incognita di primo grado e il doppio del coefficiente dell’incognita di secondo grado, – b/2a;
Nel piano cartesiano la parabola si ottiene facendo la simmetria assiale rispetto la bisettrice del primo e terzo quadrante di quella con asse parallelo all’asse delle ordinate.
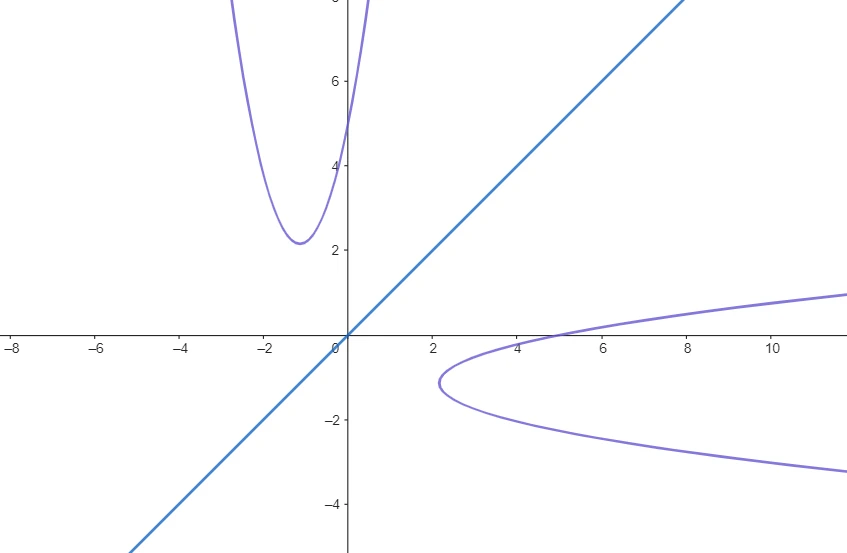
Rette e parabole
Una retta può essere rispetto una parabola:
- Esterna quando non hanno punti in comune;
- Secante quando la retta interseca la parabola in due punti e ci passa attraverso;
- Parallela nel caso in cui il punto di intersezione è solo uno;
- Tangente se il punto di intersezione è uno solo e la retta non è parallela al suo asse;
L’equazione per ricavare le coordinate dei due punti si ottiene uguagliando le equazioni della parabola e della retta e semplificandoli in un’unica equazione di secondo grado:
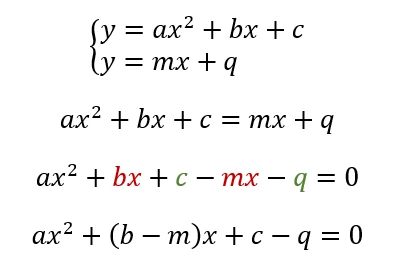
In questo caso Δ è uguale a (b-m)2 – 4a(c-q):
- Se Δ è maggiore di 0, la retta è secante;
- Se Δ è uguale a 0, la retta è tangente;
- Se Δ è minore di 0, la retta è esterna.
Per risolvere un sistema che mette a confronto l’equazione di una rette e quella di una parabola dobbiamo ricavare l’equazione di secondo grado che le unisce, ricavare le possibili incognite, sostituire i valori ottenuti nel sistema per trovare le diverse soluzioni.
Esercizio: Scopri se la retta con equazione y = x +2 è esterna, secante, tangente o parallela alla parabola di equazione y = x2 – x -1 e le coordinate degli eventuali punti di tangenza. Poi, guarda la soluzione del problema.



